Aerodynamic Design of a Windmill
Introduction 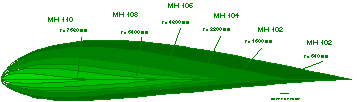
The airfoils MH 102 to MH 110 were part of the design of an optimum windmill. The windmill itself as well as the airfoils have been designed using direct inverse design methods.
Today, the design of horizontal axis windmills can be performed with good results, using inverse design methods, based on the minimum induced loss windmill, as defined by Glauert and Prandtl during the 1920s. For the analysis under off-design conditions, simple blade element methods and more complex vortex lattice methods lead to quite accurate results. The final blade geometry can be tailored exactly to the desired main operating range by using a suitable inverse design method for the airfoil sections.
 | For a small horizontal axis wind turbine, the main project data were proposed by the manufacturer, based on market studies. The basic parameters of the windmill were a constant speed generator which could be switched between two velocities of rotation and that the blade angle should be constant and not adjustable. A gearbox between power generator and the rotor of the windmill permitted the decoupling of aerodynamics and the power generator. To avoid destruction of the windmill due to over speed caused by high wind speeds, it was decided to direct the aerodynamic layout towards a stall regulated machine. (such a windmill has no variable pitch blades to control the mill at higher wind speeds; instead, the airfoils are designed to stall sharply when the operating limits are exceeded, thus limiting the power output). After some preliminary design studies, the parameters for the design, as listed below, were selected. |
| Technical Data |
| diameter | 16 m |
| gear 1 | gear 2 |
| rotor speed | 80 1/min | 120 1/min |
| at wind speed | 6.0 m/s | 9.0 m/s |
| tip Mach number | 0.2 | 0.3 |
| power loading | 450 W/m² |
| max. power output | 90 kW |
| useful wind speed range | 5 |
| stall controlled, fixed pitch, no adjustable blade angle |
Table 1: Definition of the Design Point
Regarding low manufacturing costs and competitive energy costs, the number of blades was limited to two. To achieve high yearly power on times, with short low power and non operating times, a specific power loading of 450 W/m² had been selected. A lower loading would increase the full power times, but was not possible due to a diameter restriction.
On the one hand, simple momentum theory correctly predicts maximum efficiency to occur at maximum diameter, but on the other hand the tip Mach number is directly proportional to the diameter for a fixed velocity of rotation. The tip Mach number was limited to 0.3, as a compromise between aerodynamics and noise constraints. Together with the available gearboxes, this lead to local Reynolds numbers of more than 500`000, which is sufficient to achieve high L/D ratios, which are essential for good performance.
Blade Design
The geometry of the blades is determined by the task to transform as much energy as possible from the incoming air flow into mechanical, respectively electric power. Thus the aerodynamic design of the windmill should fulfill the minimum induced loss principle. The basic aerodynamic design of the windmill was based on Glauerts optimum windmill theory, which was embedded into the framework of an existing general blade element code. This code uses two dimensional airfoil polars, which gives very good results for attached flow conditions. For cross checks, additional analysis runs were performed, using a vortex lattice code. During the preliminary design of the blades, the operating conditions for the local airfoil sections were defined in terms of Reynolds and Mach numbers as well as lift coefficient range. These conditions were used for the design of new airfoils, which were then used in the windmill design method to find the optimum blade shapes. Later additions to the code make it possible to account for the boundary layer of the ground by performing several analysis at different azimuthal blade positions.
Airfoil Design
 | Besides the number of blades, the planform and the power loading, the airfoil sections are of utmost importance for the performance of a windmill. Here maximum L/D ratios are desired to maximize efficiency, taking into account, that the surface of a wind turbine will not be perfectly smooth during the whole life span of a windmill - the airfoils should have good L over D values with rough surfaces too.
For the special case of a fixed pitch windmill, the characteristics of the airfoils are controlling the power versus wind speed performance curve. To avoid over speed conditions, the maximum power of the windmill has to be strictly limited, which can be achieved by a specially designed family of airfoils. These airfoils feature a distinct, but not necessarily hard primary stall, which leads to a limitation of the maximum power of the windmill. To avoid noise and structural problems, the airfoils have been designed to have a soft post stall plateau, followed by a soft secondary stall. The five airfoils MH 102 to MH 110 make up the new family, which shows no dramatic sensitivity with respect to surface roughness throughout the operating range. Because the preliminary windmill design and analysis defined ranges for the lift coefficient and the Reynolds number, Epplers inverse design method was ideally suited for the design of these airfoil sections. |
| 1) | 2) | 3) |
| r/R | c/R | r | c | ß | Xd | Airfoil |
| [-] | [-] | [mm] | [mm] | [°] | [mm] |
|
| 0.000 | 0.0000 | 0.0 | 0.1 | 84.500 | . | . |
| 0.040 | 0.1162 | 320.0 | 930.0 | 38.050 | . | . |
| 0.080 | 0.1094 | 640.0 | 875.1 | 25.844 | 271 | MH 102 |
| 0.120 | 0.0988 | 960.0 | 790.4 | 17.883 | . | . |
| 0.160 | 0.0917 | 1280.0 | 733.8 | 12.686 | . | . |
| 0.200 | 0.0890 | 1600.0 | 711.9 | 9.077 | 214 | MH 102 |
| 0.240 | 0.0842 | 1920.0 | 673.3 | 6.678 | . | . |
| 0.280 | 0.0814 | 2240.0 | 651.4 | 4.901 | . | . |
| 0.320 | 0.0783 | 2560.0 | 626.6 | 3.540 | . | . |
| 0.360 | 0.0745 | 2880.0 | 595.9 | 2.471 | . | . |
| 0.400 | 0.0717 | 3200.0 | 573.3 | 1.612 | 134 | MH 104 |
| 0.440 | 0.0689 | 3520.0 | 551.4 | 1.110 | . | . |
| 0.480 | 0.0668 | 3840.0 | 534.8 | 0.725 | . | . |
| 0.520 | 0.0653 | 4160.0 | 522.6 | 0.435 | . | . |
| 0.560 | 0.0643 | 4480.0 | 514.1 | 0.219 | . | . |
| 0.600 | 0.0635 | 4800.0 | 508.3 | 0.061 | 115 | MH 106 |
| 0.640 | 0.0606 | 5120.0 | 485.0 | -0.207 | . | . |
| 0.680 | 0.0579 | 5440.0 | 463.4 | -0.436 | . | . |
| 0.720 | 0.0553 | 5760.0 | 442.7 | -0.631 | . | . |
| 0.760 | 0.0528 | 6080.0 | 422.1 | -0.794 | . | . |
| 0.800 | 0.0499 | 6400.0 | 399.4 | -0.938 | 89 | MH 108 |
| 0.840 | 0.0468 | 6720.0 | 374.7 | -1.061 | . | . |
| 0.880 | 0.0429 | 7040.0 | 342.9 | -1.158 | . | . |
| 0.920 | 0.0371 | 7360.0 | 297.1 | -1.247 | . | . |
| 0.960 | 0.0280 | 7680.0 | 223.9 | -1.316 | 46 | MH 110 |
| 1.000 | 0.0000 | 8000.0 | 50.0 | -1.377 | . | . |
Table 2: Blade Geometry
- blade-angle defined by plane of rotation and x-axis of airfoil-section
- Xd - position of airfoils should form a straight line to minimize torsional Loads
- airfoil-orientation is inverse (y-axis pointing with the wind)
Performance
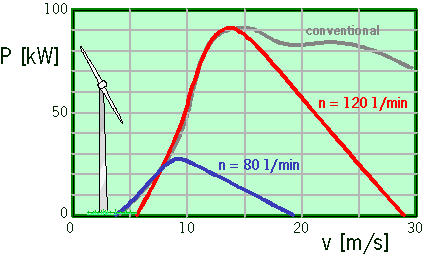
The figure below shows the power delivered by the windmill at the two velocity of rotation settings. The lower 80 rpm value is used to start up the windmill and for wind speeds up to 8 m/s, whereas the 120 rpm setting is used for wind speeds between 8 and 14 m/s. The design power of 90 kW is reached at a wind speed of 13 m/s. For comparison, the chart also contains the power curve of a windmill using conventional airfoil sections, which result in a undesired power output at higher wind speeds.
Performance chart of the optimum stall controlled windmill.
Wind Scales
Beaufort Wind Scale |
Beaufort Number
or Force | Wind Speed | Description | Effects Land / Sea |
| mph | km/hr | knots |
| 0 | <1 | <1 | <1 | Calm | Still, calm air, smoke will rise vertically. Water is mirror-like. |
| 1 | 1-3
mph | 1-5
kph | 1-3
knots | Light Air | Rising smoke drifts, wind vane is inactive. Small ripples appear on water surface. |
| 2 | 4-7
mph | 6-11
kph | 4-6
knots | Light Breeze | Leaves rustle, can feel wind on your face, wind vanes begin to move. Small wavelets develop, crests are glassy. |
| 3 | 8-12
mph | 12-19
kph | 7-10
knots | Gentle Breeze | Leaves and small twigs move, light weight flags extend. Large wavelets, crests start to break, some whitecaps. |
| 4 | 13-18
mph | 20-28
kph | 11-16
knots | Moderate Breeze | Small branches move, raises dust, leaves and paper. Small waves develop, becoming longer, whitecaps. |
| 5 | 19-24
mph | 29-38
kph | 17-21
knots | Fresh Breeze | Small trees sway. White crested wavelets (whitecaps) form, some spray. |
| 6 | 25-31
mph | 39-49
kph | 22-27
knots | Strong Breeze | Large tree branches move, telephone wires begin to "whistle", umbrellas are difficult to keep under control. Larger waves form, whitecaps prevalent, spray. |
| 7 | 32-38
mph | 50-61
kph | 28-33
knots | Moderate or Near Gale | Large trees sway, becoming difficult to walk. Larger waves develop, white foam from breaking waves begins to be blown. |
| 8 | 39-46
mph | 62-74
kph | 34-40
knots | Gale or Fresh Gale | Twigs and small branches are broken from trees, walking is difficult. Moderately large waves with blown foam. |
| 9 | 47-54
mph | 75-88
kph | 41-47
knots | Strong Gale | Slight damage occurs to buildings, shingles are blown off of roofs. High waves (6 meters), rolling seas, dense foam, Blowing spray reduces visibility. |
| 10 | 55-63
mph | 89-102
kph | 48-55
knots | Whole Gale or Storm | Trees are broken or uprooted, building damage is considerable. Large waves (6-9 meters), overhanging crests, sea becomes white with foam, heavy rolling, reduced visibility. |
| 11 | 64-72
mph | 103-117
kph | 56-63
knots | Violent Storm | Extensive widespread damage. Large waves (9-14 meters), white foam, visibility further reduced. |
| 12 | 73+
mph | 118+
kph | 64+
knots | Hurricane | Extreme destruction, devastation. Large waves over 14 meters, air filled with foam, sea white with foam and driving spray, little visibility. |
Saffir-Simpson Hurricane Scale |
Category | Wind Strength - Pressure | Effects |
1 | 65 to 83 knots
74 to 95 mph
119 to 153 kph
> 980 mb | Storm surge generally 4-5 ft above normal. No real damage to building structures. Damage primarily to unanchored mobile homes, shrubbery, and trees. Some damage to poorly constructed signs. Also, some coastal road flooding and minor pier damage. Hurricanes Allison of 1995 and Danny of 1997 were Category One hurricanes at peak intensity. |
2 | 84 to 95 knots
96 to 110 mph
154 to 177 kph
980 - 965 mb | Storm surge generally 6-8 feet above normal. Some roofing material, door, and window damage of buildings. Considerable damage to shrubbery and trees with some trees blown down. Considerable damage to mobile homes, poorly constructed signs, and piers. Coastal and low-lying escape routes flood 2-4 hours before arrival of the hurricane center. Small craft in unprotected anchorages break moorings. Hurricane Bertha of 1996 was a Category Two hurricane when it hit the North Carolina coast, while Hurricane Marilyn of 1995 was a Category Two Hurricane when it passed through the Virgin Islands. |
3 | 96 to 113 knots
111 to 130 mph
178 to 209 kph
964 - 945 mb | Storm surge generally 9-12 ft above normal. Some structural damage to small residences and utility buildings with a minor amount of curtainwall failures. Damage to shrubbery and trees with foliage blown off trees and large tress blown down. Mobile homes and poorly constructed signs are destroyed. Low-lying escape routes are cut by rising water 3-5 hours before arrival of the hurricane center. Flooding near the coast destroys smaller structures with larger structures damaged by battering of floating debris. Terrain continuously lower than 5 ft above mean sea level may be flooded inland 8 miles (13 km) or more. Evacuation of low-lying residences with several blocks of the shoreline may be required. Hurricanes Roxanne of 1995 and Fran of 1996 were Category Three hurricanes at landfall on the Yucatan Peninsula of Mexico and in North Carolina, respectively. |
4 | 114 to 134 knots
131 to 155 mph
210 to 249 kph
944- 920 mb | Storm surge generally 13-18 ft above normal. More extensive curtainwall failures with some complete roof structure failures on small residences. Shrubs, trees, and all signs are blown down. Complete destruction of mobile homes. Extensive damage to doors and windows. Low-lying escape routes may be cut by rising water 3-5 hours before arrival of the hurricane center. Major damage to lower floors of structures near the shore. Terrain lower than 10 ft above sea level may be flooded requiring massive evacuation of residential areas as far inland as 6 miles (10 km). Hurricane Luis of 1995 was a Category Four hurricane while moving over the Leeward Islands. Hurricanes Felix and Opal of 1995 also reached Category Four status at peak intensity. |
5 | 135+ knots
155+ mph
249+ kph
<> | Storm surge generally greater than 18 ft above normal. Complete roof failure on many residences and industrial buildings. Some complete building failures with small utility buildings blown over or away. All shrubs, trees, and signs blown down. Complete destruction of mobile homes. Severe and extensive window and door damage. Low-lying escape routes are cut by rising water 3-5 hours before arrival of the hurricane center. Major damage to lower floors of all structures located less than 15 ft above sea level and within 500 yards of the shoreline. Massive evacuation of residential areas on low ground within 5-10 miles (8-16 km) of the shoreline may be required. There were no Category Five hurricanes in 1995, 1996, or 1997. Hurricane Gilbert of 1988 was a Category Five hurricane at peak intensity and is the strongest Atlantic tropical cyclone of record. |
The effects described in the Saffir-Simpson scale are from the
National Hurricane Center
Dvorak Current Intensity Chart |
| The Dvorak technique is a method using enhanced Infrared and/or visible satellite imagery to quantitatively estimate the intensity of a tropical system. CI -- Current Intensity
MWS -- Mean Wind Speed
MSLP -- Mean Sea Level Atmospheric Pressure in Millibars |
| CI Number | MWS (Knots) | MSLP (Atlantic) | MSLP (Pacific) | Saffir-Simpson Category (Approximate) |
| 1 | 25 Knots |
|
|
|
| 1.5 | 25 Knots |
|
|
|
| 2 | 30 Knots | 1009 mb | 1000 mb |
|
| 2.5 | 35 Knots | 1005 mb | 997 mb |
|
| 3 | 45 Knots | 1000 mb | 991 mb |
|
| 3.5 | 55 Knots | 994 mb | 984 mb |
|
| 4 | 65 Knots | 987 mb | 976 mb | 1 (64-83 KTS) |
| 4.5 | 77 Knots | 979 mb | 966 mb | 1 (64-83 KTS);
2 (84-96 KTS) |
| 5 | 90 Knots | 970 mb | 954 mb | 2 (84-96 KTS);
3 (97-113 KTS) |
| 5.5 | 102 Knots | 960 mb | 941 mb | 3 (97-113 KTS) |
| 6 | 115 Knots | 948 mb | 927 mb | 4 (114-135 KTS) |
| 6.5 | 127 Knots | 935 mb | 914 mb | 4 (114-135 KTS) |
| 7 | 140 Knots | 921 mb | 898 mb | 5 (136+ KTS) |
| 7.5 | 155 Knots | 906 mb | 879 mb | 5 (136+ KTS) |
| 8 | 170 Knots | 890 mb | 858 mb | 5 (136+ KTS) |
Dvorak Chart from NOAA Satellite Services Division
Fujita Tornado Scale |
| F-Scale / Intensity Phrase | Wind Strength / Frequency | Description of Damage |
F0
Gale tornado | 40-72 mph
35-62 knots
64-116 kph
29% | Minimal Damage - Some damage to chimneys, TV antennas, roof shingles and windows. Breaks branches off trees, pushes over shallow-rooted trees, damages sign boards. |
F1
Moderate tornado | 73-112 mph
63-97 knots
117-180 kph
40% | Moderate Damage - Automobiles overturned, carports destroyed, trees uprooted, peels surface off roofs, mobile homes pushed off foundations or overturned, moving autos pushed off the roads. |
F2
Significant tornado | 113-157 mph
98-136 knots
181-253 kph
24% | Major Damage - Roofs torn off frame homes, sheds and outbuildings are demolished, mobile homes overturned or destroyed, boxcars pushed over; large trees snapped or uprooted, light object missiles generated. |
F3
Severe tornado | 158-206 mph
137-179 knots
254-332 kph
6% | Severe Damage - Exterior walls and roofs blown off well-built houses, metal buildings collapsed or are severely damaged, trains overturned, forests and farmland flattened, heavy cars lifted off the ground and thrown. |
F4
Devastating tornado | 207-260 mph
180-226 knots
333-419 kph
2% | Devastating Damage - Few walls, if any, standing in well-built houses, structures with weak foundations blown off some distance, large steel and concrete missiles thrown far distances, cars thrown. |
F5
Incredible tornado | 261-318 mph
227-276 knots
420-512 kph
less than 1% | Incredible Damage - Homes leveled with all debris removed, strong frame houses lifted off foundations and carried considerable distances to disintegrate. Schools, motels, and other larger structures have considerable damage with exterior walls and roofs gone, steel re-inforced concrete structures badly damaged. Automobile sized missiles fly through the air in excess of 100 meters, trees debarked. |
F6
Inconceivable tornado | 319-379 mph
277-329 knots
513-610 kph
less than 1% | These winds are very unlikely. The small area of damage they might produce would probably not be recognizable along with the mess produced by F4 and F5 wind that would surround the F6 winds. Missiles, such as cars and refrigerators would do serious secondary damage that could not be directly identified as F6 damage. If this level is ever achieved, evidence for it might only be found in some manner of ground swirl pattern, for it may never be identifiable through engineering studies |
Weather Map Wind Symbols
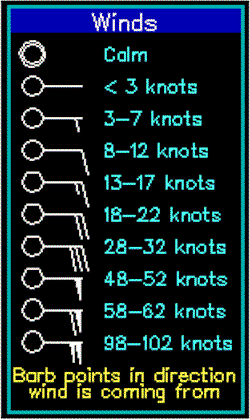
1 knot = 1 nautical mile per hour = 6076 feet per hour = 1.15078 mph
1 mph = 1 mile per hour = 5280 feet per hour = 0.86898 knots per hour
Electrical Machinery
These are the ways electrical energy and mechanical energy are transformed into each other by rotating machines
Rotating electrical machines -- generators and motors -- are devices that transform mechanical power into electrical power, and vice-versa. Electrical power from a central power station can be transmitted and subdivided very efficiently and conveniently. The operation of electrical machines is explained by four general principles, that will be briefly presented below. These principles are not difficult to understand, and illuminate most of the reasons for the stages in the historical development of electrical power, and especially of electric railways. This page discusses motors in general, but the specific application to electric locomotives is emphasized. Electricity is the medium that carries power from the prime mover, whether at a central power station or on the locomotive, to its point of application at the rail, and allows it to be controlled conveniently.
Power is rate of doing work. One horsepower means lifting 550 pounds by one foot in one second. Mechanical power is force times speed. One watt is a current of one ampere (A) flowing in a potential difference or voltage of one volt (V). Electrical power is current (in amperes, A) times voltage (in volts, V). 746W is equivalent to 1 hp. A medium-sized electric locomotive might have a rating of 2000kW, or 2680 hp. At 85% efficiency, and a voltage of 15kV, 157A is drawn from the overhead contact wire. Torque is the rotational equivalent of force, often useful in speaking of motors. It is force times perpendicular distance, and power is torque times rotational speed in radians per second.
![[Princ 1]](http://mysite.du.edu/%7Ejcalvert/tech/emprin1.gif) The first principle is that an electrical current causes a magnetic field which surrounds it like a whirlpool, and that this field, which is not material but rather a region of influence on other currents and magnets, is guided and greatly strengthened (by more than a thousand times) by passing through iron. When the current reverses in direction, so does the magnetic field. Currents deep in the earth cause its magnetic field, and the energy to drive them comes from either the rotation of the earth or the flow of heat within the earth. The field acts on the compass needle, which is a magnet. This principle can be called "electromagnet action."
The first principle is that an electrical current causes a magnetic field which surrounds it like a whirlpool, and that this field, which is not material but rather a region of influence on other currents and magnets, is guided and greatly strengthened (by more than a thousand times) by passing through iron. When the current reverses in direction, so does the magnetic field. Currents deep in the earth cause its magnetic field, and the energy to drive them comes from either the rotation of the earth or the flow of heat within the earth. The field acts on the compass needle, which is a magnet. This principle can be called "electromagnet action."
![[Princ 2]](http://mysite.du.edu/%7Ejcalvert/tech/emprin2.gif) The second is that an electrical current in a magnetic field (produced by some other currents) experiences a force perpendicular to both the direction of the current and the direction of the magnetic field, and reverses if either of these reverses in direction. The force is proportional to the current and to the strength of the magnetic field. This principle can be called "motor action."
The second is that an electrical current in a magnetic field (produced by some other currents) experiences a force perpendicular to both the direction of the current and the direction of the magnetic field, and reverses if either of these reverses in direction. The force is proportional to the current and to the strength of the magnetic field. This principle can be called "motor action."
![[Princ 3]](http://mysite.du.edu/%7Ejcalvert/tech/emprin3.gif) The third is that an electrical conductor, such as a copper wire, moving in a magnetic field has an electrical current induced in it. This is expressed by the creation of an electromotive force or voltage, which causes current to flow just as the voltage of a battery does. The effect is maximum when the wire, the motion, and the magnetic field are all mutually perpendicular. This principle can be called "generator action."
The third is that an electrical conductor, such as a copper wire, moving in a magnetic field has an electrical current induced in it. This is expressed by the creation of an electromotive force or voltage, which causes current to flow just as the voltage of a battery does. The effect is maximum when the wire, the motion, and the magnetic field are all mutually perpendicular. This principle can be called "generator action."
![[Princ 4]](http://mysite.du.edu/%7Ejcalvert/tech/emprin4.gif) And the fourth principle is that a changing magnetic field causes a voltage in any circuit through which it passes. The change can be caused by changing the current producing the magnetic field, or by moving the sources of the magnetic field. This principle can be called "transformer action."
And the fourth principle is that a changing magnetic field causes a voltage in any circuit through which it passes. The change can be caused by changing the current producing the magnetic field, or by moving the sources of the magnetic field. This principle can be called "transformer action."
A rotating electrical machine consists of a field and an armature that rotate with respect to each other. The armature is the part of the machine in which the energy conversion takes place. The field provides the magnetic field to aid this process. In DC machines, the field is stationary (the stator) and the armature rotates within it (the rotor), because the rotation is necessary to switch the armature connections by means of the commutator, but it is only the relative motion that counts. In an alternator, the armature is stationary and the field rotates. The field consists of an iron core to carry the magnetic field, and a winding to excite the magnetic field by the current passing through it (first principle). The magnetic field is a passive but essential component in the operation of the machine. Like the field, the armature also consists of iron to complete the magnetic circuit, and is separated by a short air gap from the iron of the field. It is important that the air gap be as small as possible and remain uniform as the armature rotates.
The armature also has windings. In a generator, these conductors are moved in the magnetic field producing a voltage (generator action). If a circuit is completed and current flows in these windings, a force is produced resisting the rotation of the armature (motor action) so that the driving machinery experiences a mechanical resistance and does work, which is being transformed into electrical energy. In a motor, these conductors are supplied with an electrical current, so that a force acts on them in the magnetic field (second principle), and this force can do external work. When the armature rotates while exerting the force, work is done, but a voltage is also produced opposing the applied voltage, resisting the flow of current in the armature (third principle), implying a change of electrical work into mechanical work.
This opposing voltage generated when the armature of a motor turns is called counter-electromotive force. It might seem that it resists current flow through the motor, and of course it does, but it is really the essential factor in turning electrical into mechanical energy. Only the current that is driven into a counter-emf appears as mechanical work at the motor shaft; all else is wasted, the energy going into heat instead of mechanical work. Early inventors of electric motors did not realize this, and tried simply to get as much current into the motor as possible, which only burned the motor up without producing any mechanical effect.
Current is supplied to the armature through sliding contacts formed by graphite blocks (called brushes because originally brushes of phosphor bronze wire were used instead) pressing against copper rings. It is usually necessary to change the connections of the armature windings as they rotate with respect to the magnetic field, and this can conveniently be done by making the copper rings in segments. The result is the rotary switch called the commutator. These days, semiconductor switches can be used for this purpose in small motors, eliminating the commutator, but the principle is the same. The commutator and brushes are the only parts of a machine that normally require maintenance, except for the bearings and other mechanical elements. If it is not necessary to switch the current, as in AC machines, the moving contacts are called slip rings.
Contemplate now the complete chain of energy flow from the prime mover, a steam or internal combustion engine, to the point where the mechanical power is finally applied. The transformation at each end must take place with a smooth mutual reaction, based on the second and third principles. This was not properly understood until the 1880's, so that practical electric transmission of power was delayed until that time. Power that is not delivered to the load is lost as heat in electrical resistance, which is equivalent to mechanical friction. Heat is produced in the generator, transmission lines, and motor, and limits the amount of power that can be handled.
Electrical motors were invented early, in the 1830's, as soon as the magnetic effects of electrical currents and the magnetic properties of iron became known. The motors of Christie and Pixii are typical of these, which used the repulsion and attraction between electromagnetic poles switched by a commutator. Small motors of this kind are still made for classroom demonstration. Attempts in the 1840's to make these motors more powerful and larger failed completely, because the magnetic forces do not scale proportionally to distance, and the significance of counter-emf was not known. The motors of Davenport and of Long in the United States are examples of these unsuccessful attempts to scale up classroom demonstrations to practical size.
More success was encountered in making generators, usually by moving permanent magnets (thereby creating a moving magnetic field) with respect to coils of wire wound around iron cores, to generate alternating currents for supplying arc lights and direct currents for electrolysis tanks (transformer action). These generators all ran quite hot because of their lack of efficiency, but supplied the greater currents required for these applications more cheaply than chemical batteries. This industry evolved into the electrical power industries of later years.
![[Siemens]](http://mysite.du.edu/%7Ejcalvert/tech/siemens.jpg)
![[Gramme]](http://mysite.du.edu/%7Ejcalvert/tech/gramme.jpg) Siemens and Gramme solved the problem of efficiency in the late 1870's by introducing magnetic circuits that did not change as the armature rotated, so that the electrical reactions were smooth and constant. Siemens' first machine (a generator) of 1866 is shown at the right, and a Gramme dynamo, which could also serve as a motor if the brushes were repositioned, is shown at the left. These machines had smooth armatures with conductors on their surfaces. It was still thought that the conductors actually had to be immersed in the magnetic field to produce forces. Soon it was discovered that if the conductors were put into slots in the armature surface, the same result was obtained. This was far superior mechanically, and also made a smaller air gap possible.
Siemens and Gramme solved the problem of efficiency in the late 1870's by introducing magnetic circuits that did not change as the armature rotated, so that the electrical reactions were smooth and constant. Siemens' first machine (a generator) of 1866 is shown at the right, and a Gramme dynamo, which could also serve as a motor if the brushes were repositioned, is shown at the left. These machines had smooth armatures with conductors on their surfaces. It was still thought that the conductors actually had to be immersed in the magnetic field to produce forces. Soon it was discovered that if the conductors were put into slots in the armature surface, the same result was obtained. This was far superior mechanically, and also made a smaller air gap possible.
The first long-distance transmission of electrical power took place in 1886 over the 8 km between Kriegstetten and Solothurn in Switzerland. Two Gramme machines in series were used as generators, and two similar machines in series at the other end were used as motors. The line voltage was 2000V, and the wire 6mm in diameter (1/4"). The shaft-to-shaft efficiency was 75%, and the installation remained in service until 1908.
![[Edison Z]](http://mysite.du.edu/%7Ejcalvert/tech/edisonz.jpg) Edison's famous Z-type dynamos (as direct-current generators are often called) appeared in 1879 to supply his carbon-filament incandescent lamps. These had long fields on the mistaken assumption that this gave a more powerful magnet (like a longer lever), showing how little magnetic circuits were understood at the time. This arrangement allowed a great deal of magnetic leakage between the long arms, and made the flux distribution in the armature nonuniform. Hopkinson, an engineer with Edison's British company, rationalized the field geometry, making a very good generator of the modern type a few years later. The field was symmetrical with respect to the armature, and short. A closely related type, the Manchester dynamo, is shown below. Compare its compact and short magnetic circuit with that of the Edison Z. Note the brush holder and the brass commutator on the armature. This is a two-pole machine, because the field has one N pole and one S pole.
Edison's famous Z-type dynamos (as direct-current generators are often called) appeared in 1879 to supply his carbon-filament incandescent lamps. These had long fields on the mistaken assumption that this gave a more powerful magnet (like a longer lever), showing how little magnetic circuits were understood at the time. This arrangement allowed a great deal of magnetic leakage between the long arms, and made the flux distribution in the armature nonuniform. Hopkinson, an engineer with Edison's British company, rationalized the field geometry, making a very good generator of the modern type a few years later. The field was symmetrical with respect to the armature, and short. A closely related type, the Manchester dynamo, is shown below. Compare its compact and short magnetic circuit with that of the Edison Z. Note the brush holder and the brass commutator on the armature. This is a two-pole machine, because the field has one N pole and one S pole.
![[Manchester]](http://mysite.du.edu/%7Ejcalvert/tech/manchdy.jpg) One thing that may worry you if you examine an electrical machine closely also worried early designers. They put the wires on the surface of the armature where they would actually be in the magnetic field and experience motor or generator action, in the way we have explained it here by our principles. However, wires are now always placed in slots cut in the armature iron, allowing the air gap to be made smaller and the magnetic circuit much more efficient. The overall result is the same as if the wires were actually in the magnetic field, but the mechanism is slightly different. Now the armature current in the motor magnetizes the armature iron, and the interaction of this magnet with the field poles provides the force. In a generator, the field magnetizes the armature iron, and this field moves past the conductors as the armature rotates, with an effect like a transformer. Siemens, I believe, was the one who first saw this and the great improvement it could make in electrical machines.
One thing that may worry you if you examine an electrical machine closely also worried early designers. They put the wires on the surface of the armature where they would actually be in the magnetic field and experience motor or generator action, in the way we have explained it here by our principles. However, wires are now always placed in slots cut in the armature iron, allowing the air gap to be made smaller and the magnetic circuit much more efficient. The overall result is the same as if the wires were actually in the magnetic field, but the mechanism is slightly different. Now the armature current in the motor magnetizes the armature iron, and the interaction of this magnet with the field poles provides the force. In a generator, the field magnetizes the armature iron, and this field moves past the conductors as the armature rotates, with an effect like a transformer. Siemens, I believe, was the one who first saw this and the great improvement it could make in electrical machines.
 The ways that windings of wire are arranged in modern machines are shown at the right. The windings are either around the pole pieces, or placed in slots on the surface. The part that rotates is called the rotor, and the part that remains at rest is called the stator. Both are of a magnetic core iron alloy, and are laminated if they are subject to alternating magnetic fields, to reduce eddy-current losses. DC machines typically have a salient-pole field on the stator, with the field windings on the pole pieces, and a non-salient pole winding on the armature, forming the rotor. The magnetic field of the stator is constant, while the field in the armature alternates. Therefore, the armature is laminated. The actions of salient and non-salient pole windings are equivalent. A non-salient pole winding can be arranged to give any desired spatial distribution of magnetic field. The typical salient-pole winding of a DC machine provides field-free regions between the poles that aids commutation, since switching can be done while the armature conductors are in this region and not generating any emf. In both salient and non-salient pole machines, the windings are firmly held mechanically.
The ways that windings of wire are arranged in modern machines are shown at the right. The windings are either around the pole pieces, or placed in slots on the surface. The part that rotates is called the rotor, and the part that remains at rest is called the stator. Both are of a magnetic core iron alloy, and are laminated if they are subject to alternating magnetic fields, to reduce eddy-current losses. DC machines typically have a salient-pole field on the stator, with the field windings on the pole pieces, and a non-salient pole winding on the armature, forming the rotor. The magnetic field of the stator is constant, while the field in the armature alternates. Therefore, the armature is laminated. The actions of salient and non-salient pole windings are equivalent. A non-salient pole winding can be arranged to give any desired spatial distribution of magnetic field. The typical salient-pole winding of a DC machine provides field-free regions between the poles that aids commutation, since switching can be done while the armature conductors are in this region and not generating any emf. In both salient and non-salient pole machines, the windings are firmly held mechanically.
The windings of motors and generators can be connected in one of two basic fashions. If the field windings and the armature windings are in series, they are called series-connected. In this case, the field windings are of heavy-gauge wire to carry the main motor current. The field becomes stronger as the armature current increases, leading to a very great force at low speeds. If the field and armature are in parallel, they are called shunt-connected. The field winding consists of rather fine wire. If the voltage applied to the motor is constant, then the field strength is also constant. If a generator is rotated at constant speed, then the output voltage is independent of the load. There are intermediate cases where the field has both series and shunt windings, and such machines are called compound.
Most direct-current power-station generators are mainly shunt-connected, and most traction motors mainly series-connected, as you might expect from the requirements of the two services: constant voltage in the first case, high starting torque in the second. Rotating machines can be made for voltages up to about 2000V, the restrictions being insulation and flashover at the commutator.
It is not easy to change DC voltages. One way to do this was to use a dynamotor, which had a normal field winding, but dual armature windings and two commutators. One winding was supplied at the input voltage and drove the dynamotor by motor action. The other winding supplied the output voltage. This can really be considered a kind of AC transformer. The input commutator creates AC from DC, and the output commutator changes the new AC voltage to DC. In World War II, when radios required a plate supply of, say 300 V, dynamotors were used to obtain this voltage from 6 V battery supply.
The speed of a direct-current motor is determined by both the field strength and the load. If there is no load, the speed is such that the voltage produced in accordance with the third principle exactly balances the applied voltage, and the armature current is zero. As the load is increased, the speed decreases to allow current to be drawn so the necessary electrical power can be converted. When the motor stalls, it is exerting its maximum force. Therefore, the speed of a shunt motor, or one in which the field is produced by a permanent magnet, is determined by the applied voltage, and can be adjusted finely.
If voltage is applied to a series motor without a load, the motor speeds up. As it does so, the field current decreases so the motor must speed up some more to generate the same back voltage. This keeps up until the motor flies apart. The loss of load on a series motor is a serious thing, and must be guarded against. When a loaded series motor is rotating with the maximum voltage applied to it, the current just produces the required amount of force with the existing field strength. If the field is weakened by reducing the current in it (by putting a resistance in series with it, for example) the motor must speed up to compensate. This is one method of speed control for direct-current motors.
A large direct-current motor must not be started by applying the full voltage across it while it is at rest, especially a series motor. The heavy current and field will create a great jolt that may damage the motor and its mechanical connections. A starting resistance is used to limit the initial current to only the amount necessary to put the motor into rotation. As it speeds up, the starting resistance can be removed in steps. In normal operation, the starting resistance should be removed, since it represents a significant loss of power. For further speed control when more than one motor is used, as on a streetcar or locomotive, the motors can be connected in series to start, and in parallel to run . In each case, the field can be weakened to give a higher speed. With four motors, series, series-parallel, and parallel connections, with field weakening, gives six speed levels that can be designed for service requirements. This could give, for example, speeds of 10, 15, 20, 30, 40, and 60 mph with starting resistance switched out.
A direct-current motor can be reversed by reversing the direction of the current in either the field or the armature. There is more to the story, however. The small demonstration locomotive of Werner Siemens of 1879 reversed by means of gears, and some authors have implied that it was not yet known how to reverse a DC motor, which is absurd. The problem lay in the brushes and commutator. The brushes must be placed so that their switching action takes place at the moment when the current in the windings being switched is zero. As the load on the motor increases, the armature current increases, and the magnetic field it produces causes the total magnetic field to change so that the brushes must be shifted to a new point of zero current. If this is not done, there is sparking at the commutator, which is rather destructive. The brushes on Siemens' locomotive were set at an average position for the load, so that if the motor were reversed, the brushes would have been at an improper position, and sparking would result. Therefore, he used reversing gears and the motor continued to rotate in the same direction.
A better way out of this difficulty was soon found. Small poles, called commutating poles, were placed between the main field poles. These windings are in series with the armature, and proportioned so that they cancel the varying field of the armature. The optimum brush position then becomes independent of motor load or direction of rotation.
Semiconductors have made possible a continuous control of voltage to the traction motors. This is called chopper control, and gives direct-current locomotives the same fine speed control as alternating-current locomotives. Using semiconductors, direct-current electrification is possible without any rotating machines, and all the advantages of both alternating and direct currents can be exploited.
If a commutator is not used on a generator, merely slip rings to connect with its windings without any switching, its output voltage alternates smoothly from positive to negative, which can be made to be a pretty good sine curve by using non-salient-pole windings. It is easier to generate such an alternating current by rotating the field inside a stationary armature, so that the main current does not have to flow through the sliding contacts. The sliding contacts, which are called slip rings, need handle only the lower voltage and current of the field windings. High voltages can be generated because it is much easier to insulate the stator, and because these voltages do not have to be handled by the slip rings. This is such an advantage that practically all electricity is generated as alternating current, and the generators are called alternators. These advantages were even reflected in automobiles, which previously used 6V dynamos, but now all use 12V alternators. Typically, the stators are non-salient-pole, while the rotating fields have salient poles.
Alternating current has the compelling advantage that its voltage can be changed easily and efficiently by a transformer, which is a closed iron core surrounded by two windings (first and fourth principles). The ratio of the voltages in the two windings is the same as the ratio of the number of turns, and the ratio of the currents inversely, so that the power remains the same. Since there are no mechanical parts, the efficiency of transformers is very high, and maintenance very low. Alternating current is transformed to higher voltage and smaller current for transmission, and back to lower voltages for use. Transformers with taps can be used to obtain a series of voltages if desired. In fact, an almost continuous voltage variation without loss is possible.
If direct current is required for motors, alternating current can be converted to direct current in four ways. First, a motor-generator set can be used, running at constant speed. A better solution is the rotary converter, essentially a DC generator rotated by AC supplied to it. These were the only practical ways at first for large power requirements, especially for electric railways. Later, rectifiers based on electrical discharges, notably the mercury-arc rectifier, made conversion possible without rotating machines, and with currents appropriate for locomotives. Both of these methods have now been completely superseded by solid-state (silicon) rectifiers, which are trouble-free and easily controlled. Single-phase 50/60 Hz alternating current can be supplied at high voltage, reduced in voltage by a transformer, rectified by solid state rectifiers, and applied to direct-current traction motors, making a very serviceable and economical locomotive that is today's standard.
The Ward-Leonard system of speed control for a direct current motor used a generator driven by a motor supplied from any kind of current, alternating, three-phase, or direct. By control of the generator and motor fields, control of the motor over a wide range of speeds was possible. This system was used in a few locomotives to permit the use of direct-current traction motors with single-phase alternating current supply. The problem was that three machines of equal capacity were required in place of one, a very costly alternative. Semiconductor rectifiers or chopper control have completely replaced the Ward-Leonard system.
At first sight, it would seem easy to make alternating current motors. If the polarity of the supply to a DC motor is reversed, the motor continues to turn in the same direction. If AC is supplied, the torque might be pulsating, but at least it would always be in the correct direction. Unfortunately, this is not true (except at unrealistically low frequencies) because of the existence of reactance that causes phase differences and inductive kicks. The magnetic fields and the currents get out of register, torques are small, and there are sparks everywhere. However, with the series motor there is some hope, because the same current that creates the field also passes through the armature, so they must stay in phase. In fact, series motors can be designed for AC, and they have been brought to a high state of excellence, although best at 16 2/3 or 25 Hz.
Most AC motors, however, depend on a rotating field produced in the stator, or stationary part of the motor. This is a magnetic field produced by windings through which alternating currents are passed that seems to rotate around the stator with time. The number of poles P is the number of north and south poles around the circumference, and is determined by how the windings are placed on the stator. The rate of rotation of the field is given by N = 120 f/P rpm, where f is the frequency of the alternating current. A four-pole field rotates at 1800 rpm, for example, with 60 Hz current. This is called the synchronous speed. The easiest way to produce such a field is to use an AC supply that consists of several voltages with a constant phase difference between them, called a polyphase supply. One could use two voltages at 90° phase difference, and let each voltage supply alternate coils in a four-pole machine. Better, however, to use three voltages at 120°, called three-phase, for then the power flows as evenly as with DC. These voltages are generated by separate windings on the alternator, and are supplied over three wires. These stators have no salient poles, but have a smooth surface with the windings embedded in slots. Three-phase current is normally used for transmission and distribution of electrical power, since it is the most efficient means in terms of the copper required and transmission losses.
![[3Phase]](http://mysite.du.edu/%7Ejcalvert/tech/threepha.gif)
Suppose we have such a stator with a rotating magnetic field. For the armature, we use a drum armature as for a DC motor, but simply short-circuit the windings. Then, when the motor is not rotating, we have what is very much like a transformer with a shorted secondary winding. It is excited at the frequency of the stator currents. Unlike a transformer secondary, this secondary can rotate in response to the forces exerted on it (its windings are in a magnetic field). When it does so, it tends to follow the rotating field more and more closely. When it is rotating at exactly the same speed as the rotating field, the apparent frequency to the rotor is zero, and no currents are induced at all. If it rotates slightly slower, or slips, the frequency increases, and more currents are generated. The slip is the difference in rotating speed divided by the synchronous speed, expressed as a percentage. The forces on these currents provide the torque exerted by the motor. The torque increases about proportionately to the slip. At some point, however, the reactance of the armature windings come into play not only to limit the currents, but to move them out of phase with the magnetic field. So the torque levels off, and passes a maximum value called the breakdown torque. The motor now slows down more and more rapidly, the torque more and more out of phase. When the rotor comes to rest, the starting torque is produced, and the motor will not move until the required torque is less than this amount.
This kind of motor is called an induction motor, which has no DC analog. It rotates a bit more slowly than the speed of the rotating stator field, which is called the synchronous speed. Large polyphase motors may have a slip of only 1% or so at normal load, so the induction motor is essentially a constant-speed motor. Its speed can only be greatly changed by changing the frequency of the supply. The starting torque is considerable, but at the cost of rather high currents out of phase with the voltage. The lagging power factor of an induction motor can be a problem. Nevertheless, the lack of a commutator and brushes, and that it has a reasonable starting torque, make the induction motor the most commonly used AC motor. A typical motor has a rotor composed of parallel thick copper or aluminum conductors connected to a ring of the same material at the ends. This is called a "squirrel cage" rotor.
Squirrel-cage rotors, because of their low impedance, run with small slip and give high torque at speed. However, their starting torque is poor. If your sink garbage disposal is on the same circuit with some lights, note the lights dim briefly when you switch it on. This is the result of the high reactive current drawn by the static induction motor, which can be 4 times the normal load current. Fuses must be slow-blow to let this pass before deciding that there is some problem. There is usually a circuit breaker on the disposal that opens if the motor is stalled. You might also note the limited starting torque when the motor fails to start if it gets something in its teeth. By adding resistance to the rotor, better starting torque can be obtained, at the cost of poorer running at speed. Ways have been devised to cut out the resistance after starting, but these involve a wound rotor with brushes, or complicated double windings, and have not been worth the bother.
Small single-phase induction motors can be made that create the extra phase that is necessary for starting the motor internally. Examples are the split-phase, capacitor start and shaded-pole motors used on motors of a few hp and less. Split-phase motors use a separate winding of higher inductance to produce a phase shift; capacitor motors use a capacitor for the same effect, and the capacitor can be switched out after the motor has started and has come up to speed. A shaded-pole motor has a copper ring around one side of the poles to retard the flux there, so the field appears to rotate. These single-phase motors can operate on 50/60 Hz, but are not suitable for traction motors because of their poor starting characteristics, and their low efficiency.
An unusual type of single-phase AC motor has non-salient-pole stator and rotor. The stator is supplied by the single-phase AC current, while the rotor is very similar to a DC armature, with commutator and brushes. The brushes are short-circuited, and the armature current is created by induction from the stator. If the brushes connect turns that are in field-free regions, any armature current would be in phase to produce a torque. However, with this brush position, there is no current, since the emf's cancel. If the brushes connect turns that are under the poles, the induced armature currents are a maximum, but the forces exerted on them cancel. At some intermediate brush position, there is both current and a net force. The motor can be reversed by moving the brushes past a pole to an equivalent position. Such a machine is called a repulsion motor, and it acts somewhat like a series motor. Although it gives good torque, commutation at the brushes can be difficult, with sparking. The theory of the repulsion motor is rather difficult.
A non-salient-pole stator with a rotating field can be used with a salient-pole rotor to make an AC motor. This is, in fact, exactly like an alternator except that the mechanical power is output, not input. The rotor is fed DC by slip rings to magnetize it. As the stator field rotates (electrically), it will carry the rotor poles around with it at the synchronous speed (mechanically). For this reason, this type of motor is called a synchronous motor. A synchronous motor is essentially an alternator run backwards. Rotor current must be supplied, because there is no relative motion to induce it as in an induction motor. The magnetic field in the rotor is constant, and corresponds to the constant flux in a transformer. However, its alternating variation as seen by the stator windings is now produced by its motion.
 A few poles of a synchronous motor are shown in the diagram on the left. Stator poles are shown as salient for clarity, though the stator is usually non-salient-pole. The rotor and stator poles remain in fixed relative positions. The rotor poles are carried along by the rotation, while the stator poles move as they are excited by the polyphase supply. When there is no torque exerted by the rotor, conditions are as in (a). When the motor supplies a torque, the rotor lags a bit behind, as shown in (b). The lines of force suggest the pull on the rotor, since there is a tension along the magnetic field. There is now a phase difference between rotor and stator, inducing a voltage that reduces the back emf presented to the supply, and the current to the motor stator, in phase with the voltage, must increase to bring the back emf up to the supply voltage, exactly as in a transformer. It is rather difficult to see this except by a detailed analysis involving phasor diagrams, but the force and energy relations can be verified as for a DC motor. Energy supplied against a back emf is transformed to an equal amount of mechanical enerby.
A few poles of a synchronous motor are shown in the diagram on the left. Stator poles are shown as salient for clarity, though the stator is usually non-salient-pole. The rotor and stator poles remain in fixed relative positions. The rotor poles are carried along by the rotation, while the stator poles move as they are excited by the polyphase supply. When there is no torque exerted by the rotor, conditions are as in (a). When the motor supplies a torque, the rotor lags a bit behind, as shown in (b). The lines of force suggest the pull on the rotor, since there is a tension along the magnetic field. There is now a phase difference between rotor and stator, inducing a voltage that reduces the back emf presented to the supply, and the current to the motor stator, in phase with the voltage, must increase to bring the back emf up to the supply voltage, exactly as in a transformer. It is rather difficult to see this except by a detailed analysis involving phasor diagrams, but the force and energy relations can be verified as for a DC motor. Energy supplied against a back emf is transformed to an equal amount of mechanical enerby.
The motor torque depends on the angle the rotor lags behind the rotating stator field. If the torque required is too high, the motor may drop out of synchronization, and then come to rest. Such motors can supply considerable power, but run at a fixed speed determined by the current frequency, and cannot start against a load. They may be started by an auxilary motor, by acting as an induction motor, or by other means, before load is applied. They are, therefore, unsuitable as traction motors, but can be the motor in a motor-generator set. They can drive a three-phase alternator in this arrangement, which can feed three-phase traction motors, or, of course, can drive a direct-current generator, as in a Ward-Leonard control. The synchronous motor requires DC excitation, and has slip rings to maintain, so it is not as commonly used as the induction motor. If the DC field excitation is changed, the synchronous motor can be made to draw reactive, wattless quadrature current and act as a capacitor or an inductor. Only for a certain level of excitation is the current in phase with the applied voltage. Synchronous motors without a mechanical load can be used to correct power factor in a transmission system.
One type of small synchronous motor is used to drive clocks. Tesla chose 60 Hz as the power frequency looking toward this application. More useful for this purpose are subsynchronous motors, that run at a fraction of the synchronous speed, making the gearing easier. These motors can have a toothed rotor, or a rotor consisting of copper rods, and will lock in at a subsynchronous speed, though they are fundamentally two-pole motors operating at 3600 rpm. Such motors cannot supply much torque.
A synchronous converter can convert AC to DC with high efficiency. This is a machine much like a DC generator, but with a polyphase non-salient-pole field. Polyphase, usually six-phase, power is supplied to the stator, while the rotor rotates at the synchronous speed. DC can now be taken from the commutator and brushes. The armature current is the difference of the AC and DC currents, so it is rather small and this helps the efficiency of the machine. The DC side of the machine can be used to bring it up to synchronous speed quite conveniently, if DC is available from batteries or some other source. Synchronous converters were much used before solid-state rectifiers became available.
Quite recently, semiconductors have made possible the creation of three-phase power of variable frequency, so that it becomes applicable to traction motors. Electrical power generated by an alternator, or supplied by a contact wire, is first converted to direct current, then to variable-frequency three-phase for supplying induction traction motors in a locomotive. In this way, commutators and other troublesome sliding contacts are completely eliminated, reducing maintenance costs. This has occurred even though DC has distinct advantages for traction.
Improvements in motors since the turn of the century, making them smaller, lighter, and more efficient for the same output, have been due to three main factors. The first was rational design of the magnetic circuit, to make the best use of the iron. Next was improved magnetic material, especially silicon iron with low losses, that meant less iron could be used and motors could be more compact. Finally came better insulating materials that required less room and could stand higher temperatures. These benefits extended to all other electrical machinery as well, including generating apparatus and transformers.
A supply in the range 600-700V DC was common for street railways, rapid transit, and interurban electric railways, in spite of the heavy currents required. Remember that power is voltage times current, so doubling the voltage halves the current for the same power, and the losses are proportional to the square of the current, so a decrease in current is very desirable. A voltage much above this cannot safely be used for third rails and where work must be done around energized equipment. With normal precautions, such voltages are not fatal and require actual contact for danger. 1500V was initially popular for main line electrification with an overhead contact wire. Somewhat higher voltages, up to 3000V, were later used to reduce the traction currents as far as possible, although 3000V generally requires traction motors to be permanently in series. 11, 15, and 20kV are used for alternating-current electric railways using an elevated contact wire. These are the highest voltages that can be safely used taking normal clearances into account. Personnel must be kept well out of the way of such voltages, which, unlike the lower voltages just mentioned, can reach out and be fatal at considerable distances. Transmission may be at 100kV and over, where the conductors are specially insulated on high towers.
Although we have seen a bewildering variety of rotating electrical machines, there is really only one fundamental principle at work. These machines are transformers between electrical and mechanical energy, just as the usual AC transformer transforms between electrical energy at different voltages. In fact, the ordinary transformer was also called a static transformer. These machines are dynamic transformers. On the mechanical side, the energy is transmitted by rotation. Torque times angle is work, torque times angular velocity is power. Every machine has a magnetic circuit, in which certain fluxes are established that are analogous to the flux in a static transformer. This magnetic field assists in the energy transfer, but does not receive or give energy itself. The magnetic flux links conductors, and can exert forces on them if they carry currents, and can induce emf's in them if the flux changes. The forces determine the mechanical power, while the emf's determine the electrical power. There are other energy effects, such as I2R loss in the conductors and the eddy currents, iron losses due to hysteresis, mechanical friction and windage, and the alternating flows of reactive volt-amperes. However, the induced emf's and the forces are always such as to represent an ideal conversion between electrical (emf times current) and mechanical (force times distance) energy, accompanied by these losses, which can be minimized, but are unavoidable.
When the conductors are on the surface of the rotor, actually in the magnetic field of the air gap, it is easy to see how the emf is induced, and how, if current flows, the force times distance equals the emf times current, as we pointed out at the beginning of this paper. It is not so easy to see this if the windings are on the stator, while the force is on the rotor, and if the conductors are buried in the iron, or wrapped around the poles. Nevertheless, a careful analysis would show in every case exactly the same relations that are so evident with conductors in the air gap.
To generate electrical energy, we move conductors (armature) in a magnetic field (field) at rest, or else move a magnetic field (rotor) relative to conductors at rest (stator). In either case we get a periodically reversing emf that can be made sinusoidal by careful design. If generated in the rotor, the motion can be used to switch the connections so that the output current is unidirectional, and more or less constant. Mechanical energy always enters by the rotor, but electrical energy can be taken either from the rotor or the stator. Whenever any current is drawn, the mechanical side feels the effect as an increased drag. The energy received from the mechanical side is always greater than the electrical energy delivered.
To generate mechanical energy, we can place movable conductors (armature) in a steady magnetic field (field). Torque is produced when we drive a current through the conductors, and when the armature moves, we feel an electrical opposition to supplying the current. Or, we can wind the stator to produce a rotating magnetic field, and have this field drag along conductors on a rotor. Current is driven through the rotor conductors either by induction, or by an external source. In either case, when mechanical energy is drawn, there is an electrical effect amounting to an increase of the current driven into a back emf. The energy delivered to the mechanical side is always less than the electrical energy supplied.
The only general and satisfactory way to understand the forces on the rotor of an electrical machine is by considering the magnetic field over an imaginary surface surrounding the rotor. Electric fields play no role in the forces in electrical machinery. From the magnetic field, the Maxwell stress tensor can be found, and from it the forces on the rotor, by integrating the shearing stresses over the surface. In the usual DC motor, if no armature current exists, the magnetic field passes symmetrically through the armature, and there is no net torque on it. When armature current flows, it creates a transverse component of the magnetic field, so the total field is "twisted." This field has a tangential component in the air gap that is responsible for the torque on the armature. The picture of current-carrying wires in a magnetic field is of little help in understanding an actual motor.
Rotary motion is ideal for most applications. On the mechanical side, it allows the use of an excellent and efficient mechanical transformer, gearing. Bearings provide a convenient support for rotating shafts. Turbines provide rotary power for generators, and they are efficient prime movers when used at constant speed and constant power. Just as there are reciprocating engines, one can conceive of reciprocating electrical machines. However, one notices that reciprocating motion usually has to be transformed to rotary motion for applications, aside from such things as driving a reciprocating pump. Even here, the centrifugal pump, with rotary motion, is used where possible. Reciprocating electrical machines have been tried, but were very unsatisfactory, and there is no reason to resurrect them. Motors with a linear stator would also seem quite impractical mechanically, if not electrically. The only application would be to traction, but here they are a solution without a problem. Professor E. Laithwaite of Imperial College promoted linear motors vigorously, and there are still efforts in this direction, usually with magnetic levitation as well. The best use of this idea would be if the power were supplied to the stator, with a passive "cursor," but this would be hopelessly uneconomic for practical transport, though feasible for very short distances. There is no essential difference in operation between these linear motors and the rotary ones.
a







![[Princ 1]](http://mysite.du.edu/%7Ejcalvert/tech/emprin1.gif) The first principle is that an electrical current causes a magnetic field which surrounds it like a whirlpool, and that this field, which is not material but rather a region of influence on other currents and magnets, is guided and greatly strengthened (by more than a thousand times) by passing through iron. When the current reverses in direction, so does the magnetic field. Currents deep in the earth cause its magnetic field, and the energy to drive them comes from either the rotation of the earth or the flow of heat within the earth. The field acts on the compass needle, which is a magnet. This principle can be called "electromagnet action."
The first principle is that an electrical current causes a magnetic field which surrounds it like a whirlpool, and that this field, which is not material but rather a region of influence on other currents and magnets, is guided and greatly strengthened (by more than a thousand times) by passing through iron. When the current reverses in direction, so does the magnetic field. Currents deep in the earth cause its magnetic field, and the energy to drive them comes from either the rotation of the earth or the flow of heat within the earth. The field acts on the compass needle, which is a magnet. This principle can be called "electromagnet action."![[Princ 2]](http://mysite.du.edu/%7Ejcalvert/tech/emprin2.gif) The second is that an electrical current in a magnetic field (produced by some other currents) experiences a force perpendicular to both the direction of the current and the direction of the magnetic field, and reverses if either of these reverses in direction. The force is proportional to the current and to the strength of the magnetic field. This principle can be called "motor action."
The second is that an electrical current in a magnetic field (produced by some other currents) experiences a force perpendicular to both the direction of the current and the direction of the magnetic field, and reverses if either of these reverses in direction. The force is proportional to the current and to the strength of the magnetic field. This principle can be called "motor action."![[Princ 3]](http://mysite.du.edu/%7Ejcalvert/tech/emprin3.gif) The third is that an electrical conductor, such as a copper wire, moving in a magnetic field has an electrical current induced in it. This is expressed by the creation of an electromotive force or voltage, which causes current to flow just as the voltage of a battery does. The effect is maximum when the wire, the motion, and the magnetic field are all mutually perpendicular. This principle can be called "generator action."
The third is that an electrical conductor, such as a copper wire, moving in a magnetic field has an electrical current induced in it. This is expressed by the creation of an electromotive force or voltage, which causes current to flow just as the voltage of a battery does. The effect is maximum when the wire, the motion, and the magnetic field are all mutually perpendicular. This principle can be called "generator action."![[Princ 4]](http://mysite.du.edu/%7Ejcalvert/tech/emprin4.gif) And the fourth principle is that a changing magnetic field causes a voltage in any circuit through which it passes. The change can be caused by changing the current producing the magnetic field, or by moving the sources of the magnetic field. This principle can be called "transformer action."
And the fourth principle is that a changing magnetic field causes a voltage in any circuit through which it passes. The change can be caused by changing the current producing the magnetic field, or by moving the sources of the magnetic field. This principle can be called "transformer action."![[Siemens]](http://mysite.du.edu/%7Ejcalvert/tech/siemens.jpg)
![[Gramme]](http://mysite.du.edu/%7Ejcalvert/tech/gramme.jpg) Siemens and Gramme solved the problem of efficiency in the late 1870's by introducing magnetic circuits that did not change as the armature rotated, so that the electrical reactions were smooth and constant. Siemens' first machine (a generator) of 1866 is shown at the right, and a Gramme dynamo, which could also serve as a motor if the brushes were repositioned, is shown at the left. These machines had smooth armatures with conductors on their surfaces. It was still thought that the conductors actually had to be immersed in the magnetic field to produce forces. Soon it was discovered that if the conductors were put into slots in the armature surface, the same result was obtained. This was far superior mechanically, and also made a smaller air gap possible.
Siemens and Gramme solved the problem of efficiency in the late 1870's by introducing magnetic circuits that did not change as the armature rotated, so that the electrical reactions were smooth and constant. Siemens' first machine (a generator) of 1866 is shown at the right, and a Gramme dynamo, which could also serve as a motor if the brushes were repositioned, is shown at the left. These machines had smooth armatures with conductors on their surfaces. It was still thought that the conductors actually had to be immersed in the magnetic field to produce forces. Soon it was discovered that if the conductors were put into slots in the armature surface, the same result was obtained. This was far superior mechanically, and also made a smaller air gap possible.![[Edison Z]](http://mysite.du.edu/%7Ejcalvert/tech/edisonz.jpg) Edison's famous Z-type dynamos (as direct-current generators are often called) appeared in 1879 to supply his carbon-filament incandescent lamps. These had long fields on the mistaken assumption that this gave a more powerful magnet (like a longer lever), showing how little magnetic circuits were understood at the time. This arrangement allowed a great deal of magnetic leakage between the long arms, and made the flux distribution in the armature nonuniform. Hopkinson, an engineer with Edison's British company, rationalized the field geometry, making a very good generator of the modern type a few years later. The field was symmetrical with respect to the armature, and short. A closely related type, the Manchester dynamo, is shown below. Compare its compact and short magnetic circuit with that of the Edison Z. Note the brush holder and the brass commutator on the armature. This is a two-pole machine, because the field has one N pole and one S pole.
Edison's famous Z-type dynamos (as direct-current generators are often called) appeared in 1879 to supply his carbon-filament incandescent lamps. These had long fields on the mistaken assumption that this gave a more powerful magnet (like a longer lever), showing how little magnetic circuits were understood at the time. This arrangement allowed a great deal of magnetic leakage between the long arms, and made the flux distribution in the armature nonuniform. Hopkinson, an engineer with Edison's British company, rationalized the field geometry, making a very good generator of the modern type a few years later. The field was symmetrical with respect to the armature, and short. A closely related type, the Manchester dynamo, is shown below. Compare its compact and short magnetic circuit with that of the Edison Z. Note the brush holder and the brass commutator on the armature. This is a two-pole machine, because the field has one N pole and one S pole.![[Manchester]](http://mysite.du.edu/%7Ejcalvert/tech/manchdy.jpg) One thing that may worry you if you examine an electrical machine closely also worried early designers. They put the wires on the surface of the armature where they would actually be in the magnetic field and experience motor or generator action, in the way we have explained it here by our principles. However, wires are now always placed in slots cut in the armature iron, allowing the air gap to be made smaller and the magnetic circuit much more efficient. The overall result is the same as if the wires were actually in the magnetic field, but the mechanism is slightly different. Now the armature current in the motor magnetizes the armature iron, and the interaction of this magnet with the field poles provides the force. In a generator, the field magnetizes the armature iron, and this field moves past the conductors as the armature rotates, with an effect like a transformer. Siemens, I believe, was the one who first saw this and the great improvement it could make in electrical machines.
One thing that may worry you if you examine an electrical machine closely also worried early designers. They put the wires on the surface of the armature where they would actually be in the magnetic field and experience motor or generator action, in the way we have explained it here by our principles. However, wires are now always placed in slots cut in the armature iron, allowing the air gap to be made smaller and the magnetic circuit much more efficient. The overall result is the same as if the wires were actually in the magnetic field, but the mechanism is slightly different. Now the armature current in the motor magnetizes the armature iron, and the interaction of this magnet with the field poles provides the force. In a generator, the field magnetizes the armature iron, and this field moves past the conductors as the armature rotates, with an effect like a transformer. Siemens, I believe, was the one who first saw this and the great improvement it could make in electrical machines. The ways that windings of wire are arranged in modern machines are shown at the right. The windings are either around the pole pieces, or placed in slots on the surface. The part that rotates is called the rotor, and the part that remains at rest is called the stator. Both are of a magnetic core iron alloy, and are laminated if they are subject to alternating magnetic fields, to reduce eddy-current losses. DC machines typically have a salient-pole field on the stator, with the field windings on the pole pieces, and a non-salient pole winding on the armature, forming the rotor. The magnetic field of the stator is constant, while the field in the armature alternates. Therefore, the armature is laminated. The actions of salient and non-salient pole windings are equivalent. A non-salient pole winding can be arranged to give any desired spatial distribution of magnetic field. The typical salient-pole winding of a DC machine provides field-free regions between the poles that aids commutation, since switching can be done while the armature conductors are in this region and not generating any emf. In both salient and non-salient pole machines, the windings are firmly held mechanically.
The ways that windings of wire are arranged in modern machines are shown at the right. The windings are either around the pole pieces, or placed in slots on the surface. The part that rotates is called the rotor, and the part that remains at rest is called the stator. Both are of a magnetic core iron alloy, and are laminated if they are subject to alternating magnetic fields, to reduce eddy-current losses. DC machines typically have a salient-pole field on the stator, with the field windings on the pole pieces, and a non-salient pole winding on the armature, forming the rotor. The magnetic field of the stator is constant, while the field in the armature alternates. Therefore, the armature is laminated. The actions of salient and non-salient pole windings are equivalent. A non-salient pole winding can be arranged to give any desired spatial distribution of magnetic field. The typical salient-pole winding of a DC machine provides field-free regions between the poles that aids commutation, since switching can be done while the armature conductors are in this region and not generating any emf. In both salient and non-salient pole machines, the windings are firmly held mechanically.![[3Phase]](http://mysite.du.edu/%7Ejcalvert/tech/threepha.gif)
 A few poles of a synchronous motor are shown in the diagram on the left. Stator poles are shown as salient for clarity, though the stator is usually non-salient-pole. The rotor and stator poles remain in fixed relative positions. The rotor poles are carried along by the rotation, while the stator poles move as they are excited by the polyphase supply. When there is no torque exerted by the rotor, conditions are as in (a). When the motor supplies a torque, the rotor lags a bit behind, as shown in (b). The lines of force suggest the pull on the rotor, since there is a tension along the magnetic field. There is now a phase difference between rotor and stator, inducing a voltage that reduces the back emf presented to the supply, and the current to the motor stator, in phase with the voltage, must increase to bring the back emf up to the supply voltage, exactly as in a transformer. It is rather difficult to see this except by a detailed analysis involving phasor diagrams, but the force and energy relations can be verified as for a DC motor. Energy supplied against a back emf is transformed to an equal amount of mechanical enerby.
A few poles of a synchronous motor are shown in the diagram on the left. Stator poles are shown as salient for clarity, though the stator is usually non-salient-pole. The rotor and stator poles remain in fixed relative positions. The rotor poles are carried along by the rotation, while the stator poles move as they are excited by the polyphase supply. When there is no torque exerted by the rotor, conditions are as in (a). When the motor supplies a torque, the rotor lags a bit behind, as shown in (b). The lines of force suggest the pull on the rotor, since there is a tension along the magnetic field. There is now a phase difference between rotor and stator, inducing a voltage that reduces the back emf presented to the supply, and the current to the motor stator, in phase with the voltage, must increase to bring the back emf up to the supply voltage, exactly as in a transformer. It is rather difficult to see this except by a detailed analysis involving phasor diagrams, but the force and energy relations can be verified as for a DC motor. Energy supplied against a back emf is transformed to an equal amount of mechanical enerby.